From the smartphone in your pocket to the vast power grids that span continents, the invisible force of electricity drives our modern world. At the very heart of this force lie two fundamental concepts that every electrical engineer must understand: electric charge and electric current. Charge is the intrinsic property of matter that causes it to experience a force in an electromagnetic field, while current is the directed movement of that charge.
Electric Charge
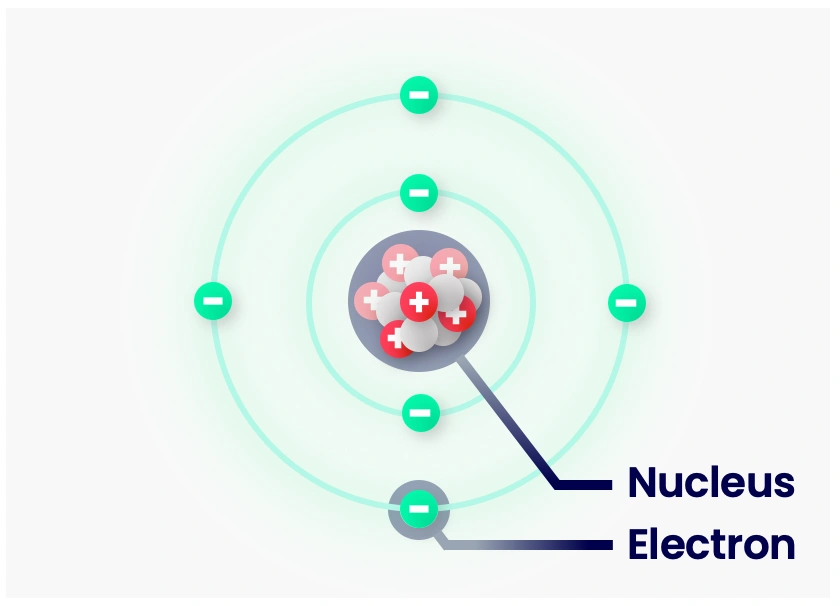
Electric charge represents one of the most fundamental properties of matter, alongside mass and time. At the atomic level, charge manifests through two distinct types of subatomic particles: protons, which carry positive charge, and electrons, which carry negative charge. This dual nature of charge creates the foundation for all electromagnetic phenomena we observe and utilize in electrical engineering applications.
The elementary charge, denoted by the symbol \(‘e’\), has a magnitude of approximately \(1.602\times 10^-19\) Coulombs. This minuscule value represents the smallest measurable unit of charge in nature. Protons possess a charge of \(+1.602\times 10^-19\) C, while electrons carry an equal but opposite charge of \(-1.602\times 10^-19\) C. Despite having identical charge magnitudes, these particles differ dramatically in mass—a proton’s mass is approximately 1,836 times greater than that of an electron. Neutrons, the third major component of atoms, carry no charge and thus do not directly participate in electrical phenomena.
The interaction between charges follows a simple principle: opposite charges attract, while like charges repel. This fundamental rule governs everything from the structure of atoms to the operation of complex electrical circuits. When two positive charges or two negative charges come into proximity, they experience a repulsive force pushing them apart. Conversely, a positive charge and a negative charge attract each other with considerable force. This behavior differs markedly from gravitational forces, which only attract and never repel.
Types and Distribution of Electric Charge
Electric charges can be categorized into several types based on their spatial distribution. Point charges represent idealized charges concentrated at a single location with negligible dimensions compared to the surrounding region. In practical applications, charges may be distributed along a line (line charge), across a two-dimensional surface (surface charge), or throughout a three-dimensional volume (volume charge). Each distribution type requires different mathematical approaches for analysis in electrical engineering calculations.
The behavior of charges also depends critically on the material containing them. In an electrically neutral object, the number of protons equals the number of electrons, resulting in zero net charge. However, when an object gains or loses electrons through various processes, it becomes electrically charged. An object with excess electrons carries a net negative charge, while one with a deficit of electrons exhibits a net positive charge.
Fundamental Properties of Electric Charge
Electric charge exhibits several remarkable properties that distinguish it from other physical quantities and make it central to electrical engineering.
1. Quantization of Charge
The quantization of charge represents one of the most important discoveries in physics. This principle states that electric charge always exists as an integer multiple of the elementary charge ‘e’. Mathematically, any charge Q can be expressed as:
\(Q=ne\)
where \(n\) is any integer (positive, negative, or zero) and \(e\) is the elementary charge. This means charges of \(1e,\,2e,\,3e,\,-5e,\) etc., can exist, but fractional charges like \(0.5e\) or \(3.7e\) cannot occur in ordinary matter. The quantization of charge was first suggested by Michael Faraday through his experimental laws of electrolysis and has since become a cornerstone principle in understanding electrical phenomena.
2. Conservation of Charge
The conservation of charge principle states that electric charge can neither be created nor destroyed—it can only be transferred from one body to another. In an isolated system, the total amount of charge remains constant over time, regardless of any internal processes or interactions.
When two neutral objects are rubbed together, electrons transfer from one to the other. The object losing electrons becomes positively charged, while the object gaining electrons becomes negatively charged. However, the total charge of the system remains zero—the positive charge on one object exactly balances the negative charge on the other. This principle underlies many practical applications, from electrostatic precipitators to charge storage in capacitors.
3. Additivity and Scalar Nature
Electric charge is a scalar quantity, meaning it has magnitude but no inherent direction. However, charges do carry algebraic signs (positive or negative), which must be considered when calculating total charges. The additivity property states that if a system contains multiple charges \(q_1,\,q_2,\,q_3,………,q_n\), the total charge \(Q\) is simply their algebraic sum:
\(Q=q_1+q_2+q_3+……+q_n\)
Coulomb’s Law: The Force Between Charges
The mathematical relationship describing the force between stationary electric charges is known as Coulomb’s Law, named after French physicist Charles-Augustin de Coulomb who published it in 1785. This fundamental law states that the electrostatic force between two point charges is directly proportional to the product of their charges and inversely proportional to the square of the distance between them.
Mathematically, Coulomb’s Law is expressed as:
\(F=k\frac{q_1 q_2}{r^2}\)
where \(F\) is the electrostatic force, \(q_1\) and \(q_2\) are the magnitudes of the two charges, \(r\) is the distance between them, and \(k\) is Coulomb’s constant with a value of approximately \(8.99\times 10^9\, Nm^2/C^2\). This constant can also be written as \(k=\frac{1}{4\pi \epsilon_0}\), where \(\epsilon_0\) is the permittivity of free space.
Several key facts emerge from Coulomb’s Law. First, the force increases dramatically when charges move closer together—doubling the distance reduces the force to one-quarter of its original value. Second, increasing either charge proportionally increases the force. Third, the force acts along the line connecting the two charges, either attracting them (for opposite charges) or repelling them (for like charges). These principles govern interactions in everything from chemical bonds to the operation of particle accelerators.
Conductors and Insulators
Materials respond very differently to the presence of electric charges, leading to their classification as either conductors or insulators. This distinction proves important in electrical engineering, determining which materials suit specific applications and how charges distribute within them.
Conductors are materials containing free electrons that can move relatively easily throughout the material. Metals such as copper, aluminum, silver, and gold exemplify excellent conductors due to their atomic structure, which features one or two loosely bound electrons in the outermost shell. These conduction electrons are not tightly bound to individual atoms and can drift through the material in response to an applied electric field. When excess charge is added to a conductor, it immediately redistributes across the surface until reaching equilibrium, with charges positioning themselves as far apart as possible due to mutual repulsion.
In contrast, insulators are materials in which electrons are tightly bound to their atoms and cannot move freely. Materials like rubber, plastic, glass, and wood serve as good insulators. When charge is added to an insulator, it tends to remain localized at the point of application rather than spreading throughout the material. This property makes insulators ideal for preventing unwanted current flow and for applications requiring charge to remain in specific locations.
Electric Current: The Flow of Charge
The definition of electric current emerges naturally from considering charge flow over time. If an amount of charge \(Q\) passes through a cross-section of a conductor during a time interval \(t\), the current \(I\) is defined as:
\(I=\frac{Q}{t}\)
Equivalently, current represents the rate of change of charge with respect to time: \(I=\frac{dQ}{dt}\).
The SI unit of current is the ampere (abbreviated as A), named in honor of French physicist André-Marie Ampère. One ampere is defined as one coulomb of charge flowing past a point per second, or \(1A=1C/s\). To put this in perspective, one ampere represents approximately \(6.242\times 10^18\) electrons flowing past a point every second.
Conventional Current vs. Electron Flow
An important distinction exists between the direction of conventional current and the actual movement of electrons. Historically, scientists defined current as the flow of positive charge from the positive terminal to the negative terminal of a voltage source. This convention was established before the discovery of electrons, when the nature of charge carriers was unknown.
However, we now know that in metallic conductors, the actual charge carriers are electrons, which carry negative charge and flow from the negative terminal toward the positive terminal. This means electron flow occurs in the opposite direction to conventional current. Despite this apparent contradiction, we continue using conventional current in circuit analysis and electrical engineering because it provides consistent and correct results.
Mechanism of Current Flow in Conductors
To Understand how current actually flows through conductors requires examining processes at the atomic level. In metallic conductors, atoms are arranged in a crystal lattice structure, with nuclei and inner electrons remaining relatively fixed in position. The outermost electrons, however, are only loosely bound and form a “sea” of free electrons that can move throughout the material.
In the absence of an applied electric field, these free electrons move randomly in all directions due to thermal energy, with velocities on the order of \(10^6\) meters per second. However, because this motion is completely random, there is no net flow of charge in any particular direction—the electrons moving in one direction are balanced by those moving in the opposite direction.
When an electric field is applied across the conductor by connecting it to a voltage source, the situation changes. The electric field exerts a force on the free electrons, causing them to drift slowly in a direction opposite to the field (since electrons are negatively charged). This drift occurs in addition to their random thermal motion. The electrons accelerate briefly under the influence of the electric field until they collide with atoms in the lattice, losing energy and changing direction. This process repeats continuously, resulting in a slow overall drift of electrons through the conductor.
Drift Velocity and Current Density
The average velocity that electrons acquire due to an applied electric field is called the drift velocity, typically denoted as \(v_d\). Remarkably, drift velocities are quite small—typically on the order of \(10^-3\) meters per second. This is millions of times slower than the random thermal velocities of the electrons. Yet despite this slow drift, electrical signals propagate through conductors at close to the speed of light because the electric field establishes throughout the conductor almost instantaneously.
The relationship between drift velocity and current is given by:
\(I=nAv_dq\)
where \(I\) is the current, \(n\) is the number density of charge carriers (electrons per unit volume), \(A\) is the cross-sectional area of the conductor, \(v_d\) is the drift velocity, and \(q\) is the charge on each carrier.
For a given conductor and voltage, the drift velocity is proportional to the applied electric field,\(v_d=\mu E\), where \(\mu\) is the electron mobility.
Current density (J) represents the current per unit cross-sectional area and relates directly to drift velocity: \(J=nv_dq\).
This quantity proves particularly useful when analyzing conductors with non-uniform cross-sections or when current distribution varies across a conductor. Current density points in the direction of current flow and has units of amperes per square meter (A/m²).
Types of Electric Current
Direct Current (DC) flows continuously in one direction through a circuit. The magnitude of DC may vary with time, but the direction remains constant. Sources of DC include batteries, solar cells, DC generators, and rectified AC power. In a DC circuit, electrons flow steadily from the negative terminal of the voltage source, through the external circuit, and back to the positive terminal.
DC proves essential for electronic devices, computers, mobile phones, and any application requiring stable, unidirectional current flow. DC can be stored in batteries and other energy storage devices, making it indispensable for portable electronics and backup power systems.
Alternating Current (AC) periodically reverses direction, with both the magnitude and direction of current changing sinusoidally over time. The frequency of AC—the number of complete cycles per second—is measured in Hertz (Hz). Most power grids operate at 50 Hz or 60 Hz, depending on the region. AC is generated by alternators (AC generators) and is the predominant form of electricity distributed to homes and industries.
The key advantages of AC include efficient long-distance power transmission and easy voltage transformation using transformers. Step-up transformers increase voltage for transmission, reducing power losses in transmission lines, while step-down transformers reduce voltage to safe levels for consumer use. This flexibility makes AC ideal for power distribution networks. However, AC cannot be directly stored and must be converted to DC for battery charging.
Ohm’s Law: The Relationship Between Voltage, Current, and Resistance
One of the most fundamental relationships in electrical engineering is Ohm’s Law, formulated by German physicist Georg Simon Ohm in 1827. Ohm’s Law describes the mathematical relationship between three key circuit parameters: voltage, current, and resistance.
Ohm’s Law states that the current through a conductor is directly proportional to the voltage across it and inversely proportional to its resistance:
\(V=I\times R\)
This equation can be rearranged to solve for any of the three variables:
\(I=\frac{V}{R}\)
\(R=\frac{V}{I}\)
These relationships reveal several important principles. First, if voltage increases while resistance remains constant, current increases proportionally. Second, if resistance increases while voltage stays constant, current decreases. Third, for a given current, higher resistance requires higher voltage.
Ohm’s Law applies strictly to ohmic materials—those where resistance remains constant regardless of voltage or current. Most metals exhibit ohmic behavior over a wide range of conditions. However, some materials and devices, such as diodes, transistors, and incandescent light bulb filaments, are non-ohmic and do not follow Ohm’s Law.
Applications of Electric Current in Daily Life
Electric current powers virtually every aspect of modern civilization, from the smallest electronic devices to massive industrial operations.
Lighting represents one of the earliest and most ubiquitous applications of electric current. Incandescent bulbs, fluorescent tubes, and modern LED lights all convert electrical energy to light, though with vastly different efficiencies. LEDs have revolutionized lighting by providing high efficiency and long lifespans, dramatically reducing energy consumption worldwide.
Heating and cooling systems depend critically on electric current. Electric heaters convert electrical energy directly to heat through resistive heating elements. Air conditioners, refrigerators, and heat pumps use electric motors to drive compressors that transfer heat from one location to another. Electric water heaters, space heaters, and industrial furnaces all rely on controlled current flow to generate precisely the amount of heat needed.
Communication systems would be impossible without electric current. Telephones, smartphones, computers, and internet infrastructure all depend on the controlled flow of current to encode, transmit, and decode information. Radio and television broadcasting, satellite communications, and fiber optic systems all use electrical signals at various stages.
Transportation increasingly relies on electric current. Electric trains and trams have used electric motors for over a century. Modern electric vehicles (EVs) store energy in batteries and use electric motors for propulsion, offering efficiency and zero-emission operation. Even traditional gasoline vehicles depend on electric current for starting, ignition, lighting, and electronic control systems.
Medical equipment represents another critical application domain. Diagnostic devices such as MRI machines, X-ray systems, and electrocardiographs use electric current to probe the human body and generate medical images. Treatment devices including defibrillators, surgical lasers, and radiation therapy equipment all depend on precisely controlled electrical currents.
Industrial manufacturing depends entirely on electric current to drive motors, control systems, and processes. Assembly lines, robotic systems, welding equipment, and computerized machine tools all require electrical power. Modern manufacturing would be completely impossible without reliable electrical current.
Example Questions on Electric Charge and Current
Q1: What is the current flowing through a circuit with a voltage of 12V and a resistance of 4Ω?
Answer: Using Ohm’s Law (\( I = \frac{V}{R} )\), we can calculate the current as:
\( I = \frac{12V}{4Ω} = 3A \)
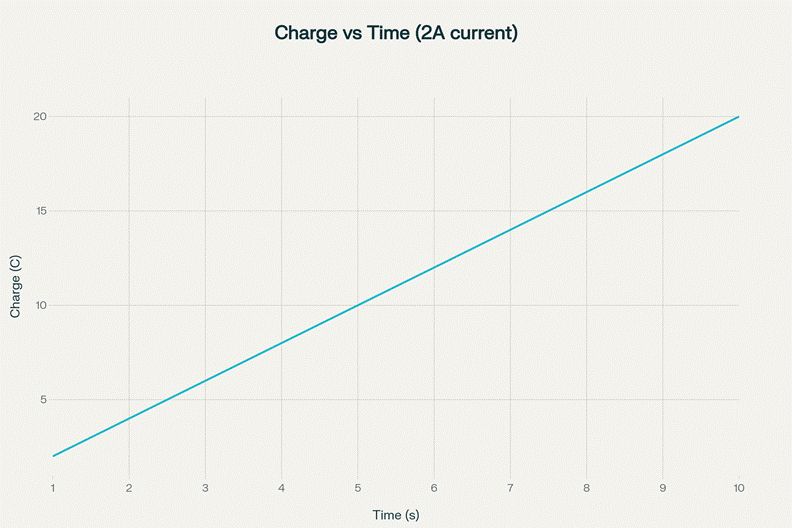
Q2: How much charge passes through a point in a circuit in 10 seconds if the current is 2A?
Answer: Using the equation for current \(( I = \frac{Q}{t} )\), we can rearrange to solve for charge \( Q \):
\(Q = I \cdot t = 2A \cdot 10s = 20C \)
Q3: What is the force between two charges of \(3 \times 10^{-6} \, C\) and \(4 \times 10^{-6} \, C\) separated by a distance of 0.5m? (Use \( k = 8.99 \times 10^9 \, Nm^2/C^2 )\)
Answer: Using Coulomb’s Law \(( F = k \frac{q_1 q_2}{r^2} )\), we can calculate the force as:
\( F = 8.99 \times 10^9 \frac{(3 \times 10^{-6})(4 \times 10^{-6})}{(0.5)^2} = 0.4316 \, N \)
Q4: If a light bulb has a resistance of 240Ω and is connected to a 120V power source, what is the current flowing through the bulb?
Answer: Using Ohm’s Law \(( I = \frac{V}{R} )\), we can calculate the current as:
\( I = \frac{120V}{240Ω} = 0.5A\)
Q5: How long will it take for a charge of 30C to pass through a point in a circuit if the current is 5A?
Answer: Using the equation for current \(( I = \frac{Q}{t} )\), we can rearrange to solve for time \( t \):
\( t = \frac{Q}{I} = \frac{30C}{5A} = 6s \)
Q6: A circuit has a current of 3A and a resistance of 10Ω. What is the voltage across the circuit?
Answer: Using Ohm’s Law \(( V = I \cdot R )\), we can calculate the voltage as:
\( V = 3A \cdot 10Ω = 30V \(
Q7: What is the power consumed by an appliance that draws 2A of current from a 220V source?
Answer: Power \( P \) is given by the product of current \( I \) and voltage \( V \):
\( P = I \cdot V = 2A \cdot 220V = 440W \)
Q8: If the distance between two charges is tripled, by what factor does the force between them change?
Answer: According to Coulomb’s Law \(( F \propto \frac{1}{r^2} )\), if the distance \( r \) is tripled, the force \( F \) will be reduced by a factor of \( 3^2 \):
\( \text{New Force} = \frac{1}{3^2} = \frac{1}{9} \)
Frequently Asked Questions
Electric charge is a basic property of matter, carried by particles like electrons and protons, that causes them to experience a force in an electromagnetic field. Electric current is the rate of flow of this charge through a conductor. In simple terms, charge is the “stuff,” and current is the “stuff in motion.”
This is a fundamental rule of electrostatics. Particles with the same type of charge (both positive or both negative) exert a repulsive force on each other, pushing them apart. Conversely, particles with opposite charges (one positive and one negative) exert an attractive force, pulling them together.
The smallest unit of charge is called the elementary charge (e), which is the magnitude of charge on a single proton or electron.
Conventional current is defined as the direction that positive charges would flow, which is from the positive terminal to the negative terminal of a power source. However, in most metal conductors, it is the negatively charged electrons that actually move, flowing from the negative terminal to the positive terminal. For historical reasons and consistency, electrical engineers almost always use the conventional current direction in circuit analysis.
The actual net forward movement of electrons in a wire, known as drift velocity, is surprisingly slow—often less than a millimeter per second. However, the electrical signal itself travels at nearly the speed of light because the electric field that pushes the electrons propagates through the wire almost instantaneously.
No, electric charge is conserved. The law of conservation of charge states that charge can neither be created nor destroyed, only moved from one place to another. In a circuit, a power source does work to move charges, but the total amount of charge remains constant.