Every electrical engineering student comes across the terms voltage, electromotive force (EMF), and potential difference early in their coursework. Most textbooks introduce these three terms in the same chapter, and many students walk away thinking they all mean the same thing. That confusion is understandable because the three concepts are closely related. However, each one has a distinct definition and a specific context where it applies.
Voltage is the informal term we use in everyday engineering conversations. EMF describes what happens inside an energy source like a battery or generator. Potential difference describes the energy relationship between any two points in a circuit or electric field. Mixing them up might not cause problems in casual discussion, but it will cause errors in circuit analysis and exam answers.
In this technical guide, we will walk you through each concept one at a time. You will find clear definitions, the formulas you need to remember, a side-by-side comparison table, and ten fully solved numerical problems. By the end of this guide, you will be able to tell exactly when to use each term and how to apply the right formula in any given problem.
1. What is Voltage?
Voltage is the electrical pressure that pushes electrons through a conducting path or circuit. Think of it like water pressure in a pipe. The higher the pressure, the more water flows. Similarly, the higher the voltage, the more current flows through a circuit.
In formal terms, voltage is defined as the work done per unit charge to move a positive test charge from one point to another in an electric field.
The mathematical expression for voltage is:
\( V = \frac{W}{Q} \)
Where:
- \(V\) = voltage in volts (V)
- \(W\) = work done in joules (J)
- \(Q\) = charge in coulombs (C)
For a resistive element that obeys Ohm’s Law, voltage can also be expressed as:
\( V = IR \)
Where \(I\) is current in amperes and \(R\) is resistance in ohms.
The equation \( V = IR \) only applies to resistive components. It is not a universal definition of voltage.
Real-world example: When you plug a phone charger into a wall outlet, the outlet provides 120V (in the US) or 230V (in the UK/EU). This voltage is the electrical pressure that drives current through your charger and into the phone battery.
2. What is Electromotive Force (EMF)?
Electromotive Force, abbreviated as EMF, is the energy per unit electric charge that a source such as a battery or generator supplies. Despite having the word “force” in its name, EMF is not a mechanical force. It is a measure of how much energy the source provides to each coulomb of charge.
EMF is the maximum voltage a source can provide when no current flows through the circuit. In other words, it is the open-circuit voltage of the source.
The formula for EMF is:
\( \varepsilon = \frac{W_{source}}{Q} \)
Where
- \(\varepsilon\) (epsilon) = EMF in volts
- \(W_{source}\) = work done by the source (e.g., chemical energy converted to electrical energy in a battery)
- \(Q\) = charge in coulombs
When current flows through a circuit, the terminal voltage of the source drops below the EMF because of internal resistance. This relationship is given by:
\( \varepsilon = V + Ir \)
Or equivalently:
\( V = \varepsilon – Ir \)
Where:
- \(V\) = terminal voltage
- \(I\) = current
- \(r\) = internal resistance of the source
Real-world example: A brand-new 9V battery has an EMF of 9V. But when you connect it to a circuit and current starts flowing, the voltage you measure at its terminals might be 8.7V or 8.8V. The missing voltage is “lost” inside the battery due to its internal resistance.
3. What is Potential Difference?
Potential difference is the difference in electric potential between two specific points in an electric field. It tells us how much work is needed per unit charge to move a positive test charge from one point to another.
The formula is the same in structure as the voltage formula:
\(V_{AB}=\frac{W_{A \rightarrow B}}{Q}\)
Where \(V_{AB}\) is the potential difference between point A and point B.
So how is this different from “voltage”? In everyday usage, voltage is simply the informal name for potential difference. When someone says “the voltage across a resistor is 5V,” they mean the potential difference between the two ends of that resistor is 5V.
Potential difference can exist even without current flowing. For example, a charged capacitor has a potential difference between its plates even when disconnected from any circuit. This is an example of a static electric field.
Real-world example: A car battery with an EMF of 12.6V might show a terminal voltage of 11.8V at its terminals when the engine is cranking. The potential difference across the starter motor might be 11.5V, and the remaining 0.3V drops across the wiring and connections. Each of these “voltages” is a potential difference between two points.
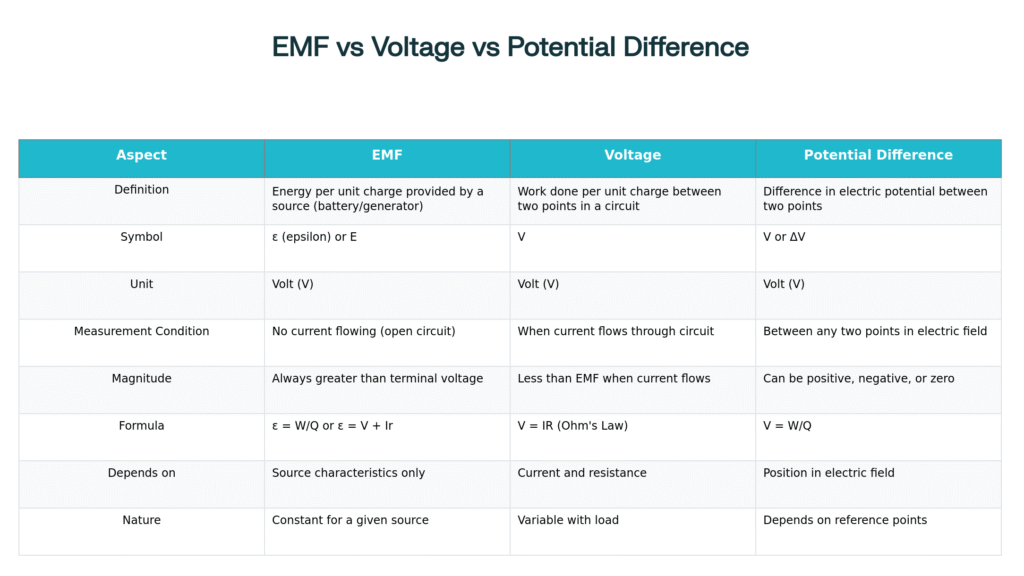
4. Differences Between EMF, Voltage, and Potential Difference
| Feature | EMF | Voltage / Potential Difference |
|---|---|---|
| Definition | Energy supplied per unit charge by a source | Work done per unit charge between two points in a circuit |
| Where it exists | Only across energy sources (batteries, generators) | Across any two points in a circuit or electric field |
| Current flow | Defined when no current flows (open circuit) | Measured when current flows through the circuit |
| Internal resistance | Includes the effect of the full energy source | Accounts for the drop due to internal resistance |
| Formula | \( \varepsilon = V + Ir \) | \( V = \varepsilon – Ir \) |
| Value | Always greater than or equal to terminal voltage | Always less than or equal to EMF |
| Nature of work | Work done by the source (chemical, mechanical, etc.) | Work done by the electric field on charges |
| Measurement | Measured in open-circuit condition | Measured under load |
The key takeaway from this table is: EMF is what the source provides. Terminal voltage is what the circuit actually receives. The difference between the two is consumed by the internal resistance of the source.
5. How to Measure Voltage, EMF, and Potential Difference
5.1 Voltage (Potential Difference) Measurement
The standard instrument for measuring voltage is the voltmeter. A voltmeter is always connected in parallel across the two points where you want to measure the potential difference. Modern digital multimeters (DMMs) include a voltmeter function along with the ability to measure current and resistance.
When using a voltmeter, always select the correct range before taking a measurement. Choosing too low a range can damage the instrument. Choosing too high a range gives less precise readings.
5.2 EMF Measurement
EMF is the open-circuit voltage of a source. There are two common methods to measure it:
- High-impedance digital voltmeter: Connect a voltmeter with very high input impedance across the terminals of the source with no load connected (open circuit). Because the voltmeter draws almost zero current, the reading closely approximates the true EMF.
- Potentiometer (classical method): A potentiometer compares the unknown EMF with a known reference voltage. At the balance point, no current flows through the source being measured. This gives a very accurate EMF reading because the voltage drop across internal resistance is zero.
5.3 Potential Difference Measurement
Since potential difference and voltage are the same thing, the measurement method is the same — use a voltmeter connected in parallel across the two points of interest.
6. Solved Numerical Problems
Problem 1: A battery has an EMF of 12V and an internal resistance of 0.5Ω. Calculate the terminal voltage when a current of 2A flows through the circuit.
Solution:
Using \(V = \varepsilon – Ir\)
\(V = 12 – (2 \times 0.5) = 11V\)
Problem 2: Calculate the potential difference if 50J of work is done to move 10C of charge between two points.
Solution:
Using \(V = \frac{W}{Q}\)
\(V = \frac{50}{10} = 5V\)
Problem 3: A cell with EMF 1.5V and internal resistance 0.2Ω supplies current to a 4.8Ω external resistance. Find the current in the circuit and the terminal voltage.
Solution:
First find current:
\(I = \frac{\varepsilon}{(R+r)} = \frac{1.5}{(4.8+0.2)} = 0.3A\)
Then find terminal voltage:
\(V = \varepsilon – Ir = 1.5 – (0.3\times 0.2) = 1.44V\)
Problem 4: Calculate EMF of a cell if terminal voltage is 9V, current is 3A, and internal resistance is 0.1Ω.
Solution:
Using \(\varepsilon = V + Ir\)
\(\varepsilon = 9 + (3 \times 0.1) = 9+ 0.3 = 9.3V\)
Problem 5: Find the work done in moving 5C charge through a potential difference of 20V.
Solution:
Using \(W = V \times Q\)
\(W = 20 \times 5 = 100J\)
Problem 6: A battery with an EMF of 9V and internal resistance of 0.5Ω is connected to a 15Ω external resistor. Find the current in the circuit and the voltage across the external resistor.
Solution:
First, find the current:
\(I=\frac{\varepsilon}{R+r}=\frac{9}{15+0.5}= \frac{9}{15.5}=0.581A\)
Then, find the voltage across the external resistor:
\(V=I\times R = 0.581\times 15 = 8.71 V\)
Alternatively, using the terminal voltage formula:
\(V=\varepsilon – Ir = 9-(0.581\times 5) = 9- 0.29 = 8.71 V\)
Both methods give the same answer, which confirms the result.
Problem 7: A point charge of \(3\times 10^{-6}\,C\) is located 0.1 m away from another point charge of \(−2\times 10^{−6}\, C\). What is the electric potential at the midpoint between the two charges? (Use \(k=9\times 10^9 N m^2/C^2\))
Solution:
The midpoint is at a distance of 0.05 m from each charge.
Electric potential due to the first charge at the midpoint:
\(V_1=\frac{kq_1}{r}= \frac{(9\times 10^9)(3\times 10^{-6})}{0.05} = 540,000\,V\)
Electric potential due to the second charge at the midpoint:
\(V_2=\frac{kq_2}{r}= \frac{(9\times 10^9)(-2\times 10^{-6})}{0.05} = -360,000\,V\)
Total electric potential at the midpoint:
\(V = V_1+V_2 = 540,000+(-360,000)=180,000V\)
Problem 8: Two batteries are connected in series. Battery A has an EMF of 6V and an internal resistance of 0.1Ω. Battery B has an EMF of 9V and an internal resistance of 0.3Ω. Find the total EMF and total internal resistance of the combination.
Solution:
For batteries in series, both EMF and internal resistance add up.
Total EMF:
\(\varepsilon_{total}=\varepsilon_1+\varepsilon_2=6+9=15\,V\)
Total internal resistance:
\(r_{total}=r_1+r_2=0.1+0.3=0.4\,\Omega\)
Problem 9: A battery with an EMF of 24V and internal resistance 0.8Ω is connected to two resistors in series: R1=5Ω and R2=7Ω. Find the current in the circuit, the terminal voltage of the battery, and the voltage drop across each resistor.
Solution:
Total external resistance:
\(R_{total}=R_1+R_2=5+7=12\Omega\)
Current in the circuit:
\(I=\frac{\varepsilon}{R_{total} + r}=\frac{24}{12+0.8} = \frac{24}{12.8}=1.875\,A\)
Terminal voltage:
\(V=\varepsilon – Ir = 24-(1.875\times 0.8)=24-1.5=22.5\,V\)
Voltage drop across \(R_1\):
\(V_1=IR_1=1.875\times 5=9.375\,V\)
Voltage drop across \(R_2\):
\(V_2=IR_2=1.875\times 7=13.125\,V\)
Verification: \(V_1+V_2=9.375+13.125=22.5\,V\), which equals the terminal voltage.
Problem 10: A 6V battery with internal resistance 0.6Ω is connected to a 2.4Ω external resistor. Calculate the power dissipated in the external resistor and the power wasted inside the battery.
Solution:
Current in the circuit:
\(I=\frac{\varepsilon}{R+r}= \frac{6}{2.4+0.6}= \frac{6}{3}= 2\,A\)
Power dissipated in external resistor:
\(P_{external}=I^2R=2^2\times 2.4=9.6\,W\)
Power wasted inside the battery:
\(P_{internal}=I^2r=2^2\times 0.6=2.4\,W\)
7. Conclusion
EMF is the total energy per unit charge supplied by a source like a battery or generator. It is measured under open-circuit conditions when no current flows. Terminal voltage is the actual voltage available at the terminals of the source when current is flowing, and it is always less than the EMF due to the internal resistance of the source. Potential difference is the general term for the voltage between any two points in a circuit or electric field, and in everyday usage, “voltage” and “potential difference” mean the same thing.
8. Frequently Asked Questions (FAQs)
EMF is the energy per unit charge that a source provides when no current flows through the circuit. Voltage (terminal voltage) is the actual potential difference available at the terminals of the source when current is flowing. EMF is always equal to or greater than terminal voltage during discharge because some energy is lost to internal resistance.
EMF is greater because voltage drops due to internal resistance when current flows, following V = EMF – Ir
Yes. A charged capacitor has a voltage (potential difference) across its plates even when it is disconnected from any circuit and no current flows. Similarly, a battery sitting on a shelf has an EMF across its terminals with no current flowing.
When the load resistance decreases (meaning more load is added in a parallel configuration), the current in the circuit increases. A higher current means a larger voltage drop across the internal resistance (Ir). This reduces the terminal voltage. That is why a battery’s voltage “sags” under heavy load.
No. The name “electromotive force” is a historical term that has stuck around. EMF is measured in volts, not in newtons. It is energy per unit charge, not a force.
The most straightforward method is to connect a high-impedance digital voltmeter across the terminals of the source with no load attached (open circuit). Since the voltmeter draws almost no current, the reading is very close to the true EMF.
Yes. In circuit analysis, if you assign a current direction that opposes the polarity of the battery, the EMF appears as a negative value in your equations.