When working with alternating current (AC) systems, electrical engineers must understand how to characterize waveforms that continuously vary with time. Unlike direct current (DC), which maintains a constant magnitude, AC quantities require specific mathematical approaches to quantify their effectiveness and behavior. Three fundamental parameters define any AC waveform: Peak Value, Average Value, and Root Mean Square (RMS) Value. These values are essential for power calculations, circuit design, equipment sizing, and safety considerations in electrical engineering applications.
What is Peak Value?
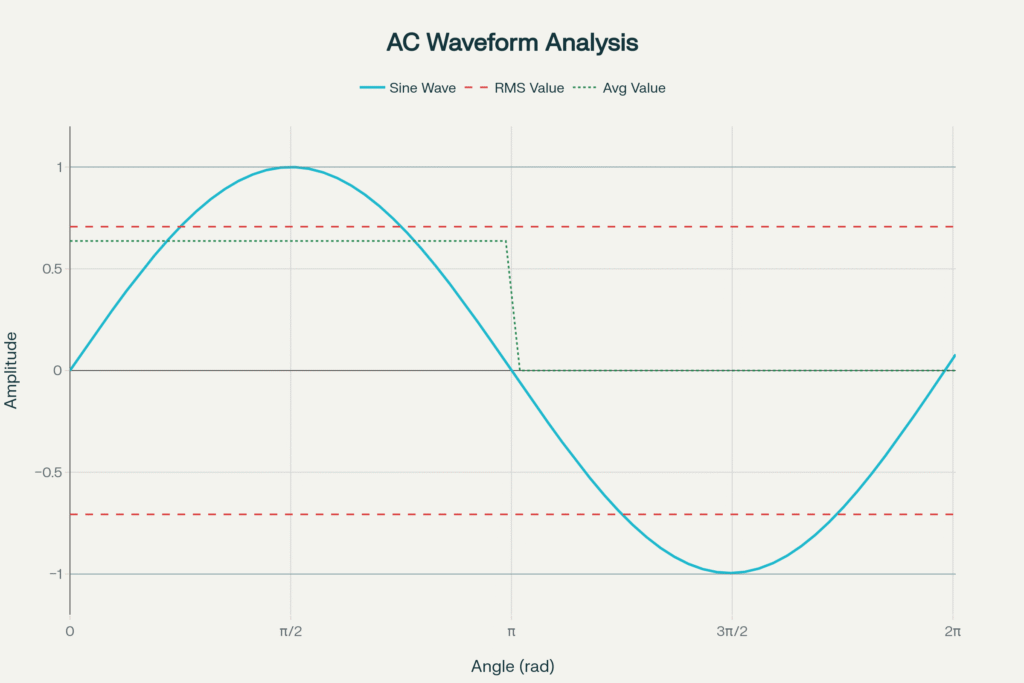
Peak value represents the maximum instantaneous amplitude that an AC waveform reaches during one complete cycle. Also known as the maximum value or amplitude, it indicates the highest positive or negative excursion from the zero reference line. For a sinusoidal waveform described by \(v(t)=V_{m}sin(ωt)\), the peak value is \(V_{m}\).
The peak value is crucial for several engineering applications. In high-voltage systems, insulation design must consider peak voltages rather than RMS values to prevent breakdown. Similarly, when selecting capacitors for rectifier circuits, the peak voltage rating determines the component’s ability to withstand maximum stress. The peak-to-peak value, representing the total voltage swing from positive to negative peak, equals twice the peak value for symmetrical waveforms.
For sinusoidal signals, the relationship between peak and RMS values remains constant:
\(V_{peak}=\sqrt{2}\times V_{RMS}=1.414×V_{RMS}\)
What is Average Value?
The average value of an AC waveform represents the arithmetic mean of all instantaneous values over a specified time period. For symmetrical AC waveforms like pure sine waves, the average value over a complete cycle equals zero because positive and negative half-cycles cancel each other. Therefore, average values are typically calculated over half-cycles or for rectified waveforms where this cancellation doesn’t occur.
For a sinusoidal waveform, the average value over a positive half-cycle is given by
\(V_{avg}=\frac{2}{\pi} \times V_{m}=0.637 V_{m}\)
This value represents the equivalent DC level that would produce the same net effect as the AC signal’s positive portion. In rectifier circuits, where AC is converted to pulsating DC, the average value becomes particularly important for determining the DC output level.
Average values find practical application in power supply design, where engineers need to determine filtering requirements and output voltage levels. Digital multimeters that use average-responding circuits rely on this principle, measuring the average value and scaling it to display an equivalent RMS reading for sinusoidal inputs.
Root Mean Square (RMS) Value: The Effective Value
The RMS value stands as the most significant parameter for electrical engineering calculations. Defined as the square root of the mean of the squares of all instantaneous values, RMS represents the equivalent DC value that would produce the same power dissipation in a resistive load. This makes RMS the “effective value” of an AC quantity.
Mathematically, for any periodic waveform \(v(t)\), the RMS value is calculated as:
\(V_{RMS}=\sqrt{\frac{1}{T}\int_{0}^{T} v^2(t)dt}\)
For sinusoidal waveforms, this simplifies to \(V_{RMS}=\frac{V_{m}}{\sqrt{2}}=0.707 V_{m}\)
This relationship stems from the fundamental definition that RMS values enable direct power calculations using familiar DC formulas like \(P=V^2/R\) and \(P=I^2R\).
The practical significance of RMS values cannot be overstated. All AC voltage and current ratings on electrical equipment represent RMS values. The standard household voltage of \(120V\) or \(230V\) refers to RMS values, with corresponding peak values of approximately \(170V\) and \(325V\) respectively. This standardization allows engineers to perform power calculations and equipment sizing using straightforward DC-equivalent formulas.
Form Factor and Crest Factor: Waveform Shape Indicators
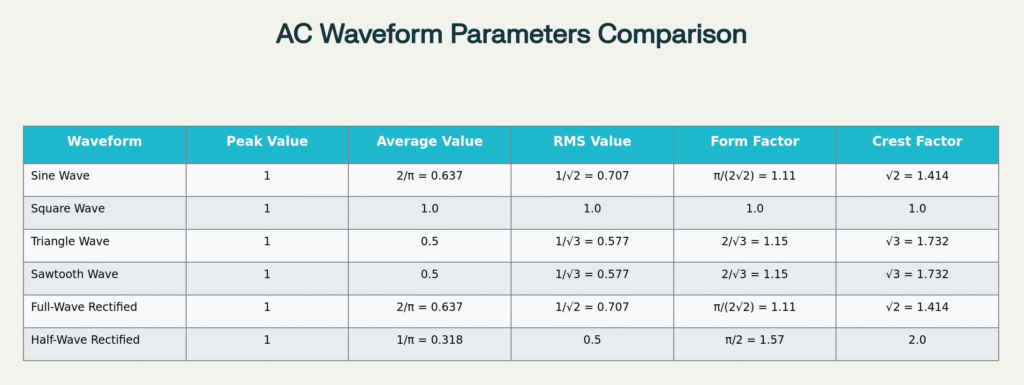
Two additional parameters help characterize waveform shapes beyond the basic peak, average, and RMS values. The Form Factor represents the ratio of RMS value to average value: \(FF=V_{RMS}/V_{avg}\). For sinusoidal waveforms, the form factor equals \(\frac{\pi}{2 \sqrt{2}}=1.11\).
The Crest Factor (or Peak Factor) defines the ratio of peak value to RMS value: \(CF=V_{peak}/V_{RMS}\). For sine waves, the crest factor equals \(\sqrt{2}=1.414\). Higher crest factors indicate sharper peaks, which can impact power quality and equipment performance in electrical systems.
Measurement and Instrumentation
Modern electrical measurements require understanding the differences between various meter types. Average-responding multimeters measure the average value of rectified AC signals and scale the result to display an RMS equivalent. These instruments provide accurate readings for pure sinusoidal waveforms but can introduce significant errors (up to 40%) when measuring distorted or non-sinusoidal signals.
True RMS multimeters directly calculate the RMS value using sophisticated analog or digital processing circuits. These instruments accurately measure both sinusoidal and non-sinusoidal waveforms, making them essential in modern electrical systems containing variable frequency drives, switching power supplies, and other non-linear loads.
Conclusion
Peak Value, Average Value, and RMS Value represent fundamental concepts that every electrical engineer must master for effective AC system analysis and design. Peak values determine insulation requirements and component stress levels, while average values relate to rectified DC output levels. RMS values, being the most practical for power calculations, serve as the standard for equipment ratings and electrical system design.